
L'application EDITEQUA, écrite en Visual Basic 6.0, nécessite
l'INSTALLATION PREALABLE de SV3 et de SV5.
Il faudra aussi installer le dossier
SYSDYN dans SV3\MATHVOX.
Si vous avez déjà installé SV5 (et donc SV3) passez à l'installation de EDITEQUA.
Lors de la décompression des fichiers suivants, on vous demandera un nom de répertoire:
vous devrez OBLIGATOIREMENT entrer c:\
pour un fonctionnement correct.
Les installations suivantes créent uniquement les deux répertoires c:\sv3 et c:\sv5.
La désinstallation COMPLETE ne demande donc que la suppression de ces deux répertoires.
téléchargement et installation de SV3
téléchargement et installation de SV3\MATHVOX\SYSDYN
téléchargement et installation de SV5 (bien penser à télécharger SV3 avant SV5)
Vous pouvez maintenant procéder à l'installation de EDITEQUA
téléchargement et installation de EDITEQUA
(21/05/07: nouvelle
installation
facile avec un seul fichier setup)
Une fois téléchargé, il suffit d'exécuter le setup (setupeditequa.exe) qui installera le projet editequa dans votre répertoire Program Files; la désinstallation TOTALE d'editequa se fera classiquement par Ajout Suppression de Programmes dans le Panneau de Configuration.
Le logiciel EDITEQUA réalise une analyse
formelle des systèmes différentiels ordinaires d’ordre un dans R2
à second membres polynômiaux de la forme:
dx/dt = f(x, y)
dy/dt = g(x, y)
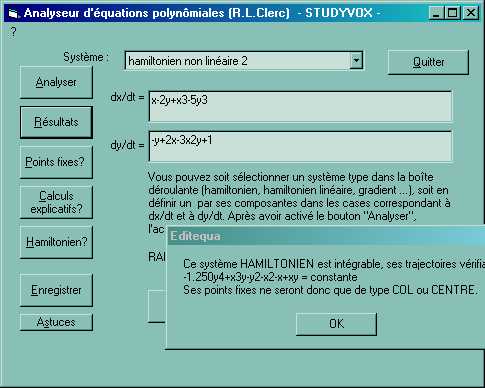
Après la saisie des seconds membres f(x,y) et g(x, y),
le bouton Analyser enclenche le processus d’étude
du système: dès que l’ analyse générale du système est terminée, une fenêtre OK
vous le dit, et aussitôt après une autre fenêtre OK vous annonce que la
recherche des points fixes est terminée.
Les boutons 'Résultats', 'Points fixes?', 'Hamiltonien?' ou 'Calculs
explicatifs?' donnent alors les informations concernant votre
système que vous pourrez aussi enregistrer avec le bouton
Enregistrer (à condition d’avoir auparavant sélectionné
'nouveau système' dans la boîte déroulante);il se trouvera
dès la prochaine activation du logiciel dans la boîte déroulante 'Système'.
Attention à la notation concernant les
puissances; pour une variable on notera x3 ou y5, mais pour une quantité
entre parenthèses on écrira (x2+3y)²3 ou
(2x-y3)²4, le ² exprimant l’opération puissance.
Quelques rappels théoriques
    |